Audio File Format Unpacking
A common place to encounter proprietary, undocumented multimedia formats is the data files of various computer games. That was the case with SWAT 3 released by Sierra back in 2001.
Over the years, many of the file formats used by the game were reverse engineered, while the custom audio format CMP still remained unknown. Sierra provided a “Compsound” tool to compress WAV files to CMP format, but the reverse was impossible unless playing the sounds in-game. This article aims to describe the process used to reverse engineer the CMP format.
First impressions
Compsound is a relatively simple program which encodes individual WAV files to the CMP format used in SWAT 3. We will use Audacity to generate some test sounds for encoding, all of which will be 16 bit PCM, 100 milliseconds and 44100 Hz sampling frequency. The sounds are: 220 Hz sawtooth wave, 440 Hz sine wave and random white noise.
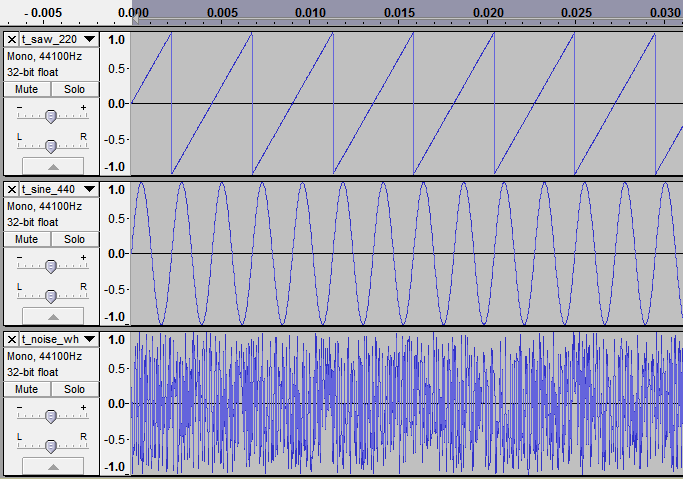
I did not know beforehand if the compression was lossless or not, but encoding the white noise answered the question immediately: the size was reduced from 8864 to 7232 bytes. However the sawtooth waveform was reduced from 8864 to 1504 bytes. Clearly the compression is somehow adaptive to the complexity of the input.
Let’s see what kind of headers the files have. Here is the beginning of t_saw_220hz.cmp:
00000000 44 4e 53 45 00 01 00 00 c0 05 00 00 74 22 00 00 |DNSE........t"..|
00000010 44 ac 00 00 10 00 00 00 00 00 00 00 00 00 00 00 |D...............|
00000020 12 0d 82 84 83 03 0e 38 38 e0 80 03 0e 0e 38 38 |.......88.....88|
00000030 38 80 83 83 03 0e 38 38 e0 e0 00 0e c6 01 d0 7f |8.....88........|
00000040 07 00 05 40 00 10 40 00 16 04 68 04 42 02 07 1c |...@..@...h.B...|
00000050 70 70 70 c0 01 07 07 1c 70 c0 c1 01 07 07 07 70 |ppp.....p......p|
00000060 70 c0 c1 01 07 1c 1c 70 70 c0 c1 01 07 1c 70 70 |p......pp.....pp|
00000070 c0 c1 01 07 07 1c 70 70 c0 c1 01 1c 1c f0 f6 ff |......pp........|
00000080 fd 3f 00 12 81 00 6e 20 a0 80 60 20 02 07 1c 1c |.?....n ..` ....|
00000090 70 70 c0 c1 01 07 1c 70 70 70 c0 01 07 1c 1c 70 |pp.....ppp.....p|
000000a0 c0 c1 c1 01 07 1c 1c 70 c0 c1 01 07 1c 1c 70 c0 |.......p......p.|
000000b0 c1 01 07 07 1c 70 70 70 c0 01 07 1c 1c 8c 07 a0 |.....ppp........|
The presence of repetitive patterns indicates no encryption or strong compression is used which makes things much easier for us. Upon examining multiple files, it became evident that the CMP files have a fixed header of 32 bytes after which the compressed stream follows. The header is structured as follows:
| Bytes | Type | Content |
|---|---|---|
| 8 | constant | 44 4e 53 45 00 01 00 00 |
| 4 | integer, little endian | size of compressed CMP stream in bytes |
| 4 | integer, little endian | size of uncompressed WAV stream in bytes |
| 4 | integer, little endian | sampling frequency in Hz |
| 12 | constant | 10 00 00 00 00 00 00 00 00 00 00 00 |
There’s no indication that the CMP format is capable of properly encoding any other than mono sound. Moving further, the stream itself gives few clues to go on, and I did not notice any common structure with the other test files. That means better tools need to used.
Reverse engineering with IDA Pro
Compsound.exe is a relatively small executable. At only 540 kB, the majority of the space is actually occupied by image resources which leaves only around 100 kB for code.
When opening Compsound.exe in IDA Pro, it can be seen that 302 functions were recognized, and library functions were automatically colored blue:
To find the compression function, we want to be looking for a relatively large function which does file reading calls in a loop. In C++ executables the library calls are obfuscated by the use of function pointers, so we can’t immediately see where such calls are being made.
We can however use a trick and search for any constants seen in the CMP headers. Recall that the files start with the bytes 44 4e 53 45. We can flip the byte order and use ALT+I to search for immediate values of 0x45534E44. Sure enough, two functions were found:
Address Function Instruction
------- -------- -----------
.text:00403CE2 sub_403BB0 mov [esp+88h+var_2C], 45534E44h
.text:00404259 sub_404200 cmp [esp+0A0h+var_84], 45534E44h
mov instruction might mean the header is being written in the function, while cmp might check for incompatible headers in input files (CMP files can’t be encoded twice). Indeed, it can be seen the only call being made to sub_404200 is in a branch statement in sub_403BB0. Let’s rename sub_403BB0 to InitializeFiles. After examining and renaming neighboring functions we can draw the following xrefs chart:
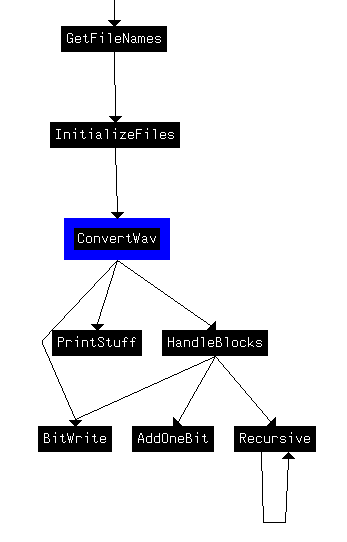
Many of these names weren’t immediately obvious looking at the contents. Basically most of the conversion process happens in the calls being made in HandleBlocks. Let’s look at it with the default variables:
int __stdcall HandleBlocks(int a1, int *a2, int a3, int a4, int a5)
{
int v5; // esi@1
int v6; // edi@1
int v7; // ebx@1
int v8; // eax@4
int v10; // [sp+20h] [bp+10h]@1
v5 = a4;
v6 = *a4;
v7 = 0;
sub_4033A0(a2, a3, *a4, a5, a4);
v10 = *a2;
if ( v6 != *v5 )
{
sub_4039C0(1);
sub_403A20(0, v6);
sub_403A20(*v5, 4);
v7 = *v5 + 5;
}
if ( v10 < 0 )
{
sub_4039C0(1);
v8 = -v10;
}
else
{
sub_4039C0(0);
v8 = v10;
}
sub_403A20(v8, *v5);
return *v5 + v7 + 1;
}
Not very clear. When we examine the subfunctions and rename variables, the picture becomes much more simple:
int __stdcall HandleBlocks(int *buffer, int *table, int C25, int *len, int C1)
{
int len_old; // edi@1
int extra_len; // ebx@1
unsigned int bits; // eax@4
int val; // [sp+20h] [bp+10h]@1
len_old = *len;
extra_len = 0;
Recursive(table, C25, *len, C1, len);
val = *table;
if ( len_old != *len )
{
AddOneBit(buffer, 1); // AddOneBit writes the stop bits
BitWrite(buffer, 0, len_old);
BitWrite(buffer, *len, 4u);
extra_len = *len + 5;
}
if ( val < 0 )
{
AddOneBit(buffer, 1);
bits = -val;
}
else
{
AddOneBit(buffer, 0);
bits = val;
}
BitWrite(buffer, bits, *len); // zero codewords not written with previous 1
return *len + extra_len + 1;
}
The CMP format uses variable bit length codes to encode the PCM samples. It cleverly uses both the stop bit and zero codeword to indicate whether the next value is a normal codeword or a new length to be encoded in the stream. This means the decoding process must work exactly, or else the stream might become de-synced and corrupt the rest of file.
We still don’t know what the codewords actually represent. The function Recursive has a complicated structure with thousands of calls being made, so it’s not clear what the algorithm is actually doing. To gain more insight, we can use the debugger to capture the arguments to both AddOneBit and BitWrite while the program is encoding the test WAV files.
Let’s assign a breakpoint at the beginning of BitWrite with the condition:
Message("%d %d\n", Dword(ESP+8), Dword(ESP+4)), 0
And AddOneBit:
Message("1 %d\n", Dword(ESP+4)), 0
The trailing 0 tells IDA to continue immediately after breaking, so we’ll just get the codestream in the log window. First number is the bit count written to the buffer and second is the actual value. With t_noise_white.wav it starts with:
1 1
0 0
4 8
1 1
8 209
1 1
8 0
4 10
1 0
10 646
1 1
10 655
1 1
10 798
1 1
10 0
4 11
1 0
11 1166
This actually shows the code length was changed to 8 and then to 10. If we ignore the stop bits and length re-encodings, the actual codewords next to the real PCM samples look like:
CMP WAV
-209 -6691
646 7285
-655 335
-798 -32200
1166 -27404
72 -20297
-320 -23433
154 -21630
1207 18783
-2288 -14022
2280 26165
-1568 16145
-24 5332
-574 -23821
1089 -18128
197 -6123
683 27754
-1967 -1339
75 -28032
1233 -15270
1097 32616
-2187 10490
We’re onto something here. The sign bit seems to relate to increasing and decreasing values in the PCM samples. The magnitude is a bit off because the lossy compression removes some low-order bits. Can it be that the codewords encode differences between subsequent PCM samples? No, the values of 1166 and 72 encode somewhat similar changes in PCM values.
What if the codewords actually encode difference to previous difference between subsequent samples? Let’s correct the magnitude with shifting by 5 bits and calculate:
delta = 0
previous sample = 0
for each codeword:
delta += codeword
next sample = previous sample + delta
Now we get:
CMP WAV
-6688 -6691
7296 7285
320 335
-32192 -32200
-27392 -27404
-20288 -20297
-23424 -23433
-21632 -21630
18784 18783
-14016 -14022
26144 26165
16128 16145
5344 5332
-23808 -23821
-18112 -18128
-6112 -6123
27744 27754
-1344 -1339
-28032 -28032
-15264 -15270
32608 32616
10496 10490
That is definitely the compression method. Using this information, the decompression tool can be written relatively easily in Python 3. It is included below along with the test files. It can be used in Linux or Windows Git Bash environments.